The built-in Python complex() function makes it easy to work with complex numbers. When dealing with mathematical operations in Python, there are times when you will need to use complex numbers. Complex numbers consist of a real part and an imaginary part, and they help solve various mathematical problems. In this article, we will explain the basic usage of the complex() function and explore different ways to utilize it.
Table of Contents
What is the Python complex() function?
The complex() function is used in Python to generate complex numbers. A complex number consists of a real part and an imaginary part. While the imaginary part is usually represented by “i”, in Python, “j” or “J” is used. Complex numbers can be written in the following form:
a + bjWhere a is the real part, and b is the imaginary part.
Basic Usage
The complex() function can take two parameters. The first parameter is the real part, and the second parameter is the imaginary part. For example, to create a complex number with a real part of 2 and an imaginary part of 3, you can write:
z = complex(2, 3)
print(z)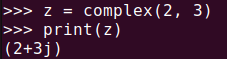
complex() functionIf you provide only one parameter, it will be considered the real part, and the imaginary part will automatically be set to 0.
z = complex(4)
print(z)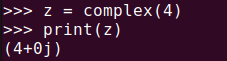
complex() functionYou can also create a complex number using a string.
z = complex("2+3j")
print(z) # output: (2+3j)Separating Real and Imaginary Parts
It’s very simple to separate the real and imaginary parts of a complex number. The complex object provides the real and imag attributes, which allow you to access the real and imaginary parts, respectively.
z = complex(5, 8)
print("Real part:", z.real) # Output: Real part: 5.0
print("Imaginary part:", z.imag) # Output: Imaginary part: 8.0This allows you to handle complex numbers more effectively by accessing their individual components.
Using Complex Numbers in Python
Complex Number Operations
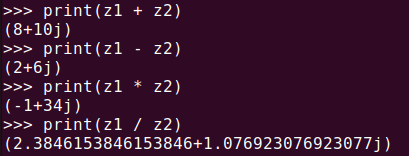
Complex numbers support all basic mathematical operations such as addition, subtraction, multiplication, and division.
z1 = complex(5, 8)
z2 = complex(3, 2)
print(z1 + z2)
print(z1 - z2)
print(z1 * z2)
print(z1 / z2)As shown, basic arithmetic operations between complex numbers are easily handled in Python.
complex() functionFinding the Absolute Value of a Complex Number
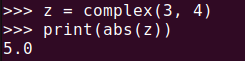
The absolute value of a complex number can be found using the abs() function. The absolute value represents the distance from the origin to the complex number and can be calculated using the following formula:
|z| = sqrt(a^2 + b^2)Where a is the real part, and b is the imaginary part. You can use the built-in abs() function in Python to calculate the absolute value of a complex number as follows:
z = complex(3, 4)
print(abs(z))This result is the same as the one obtained using the Pythagorean theorem.
abs() functionMore Complex Use Case: Rotating Coordinates
Complex numbers can also be used to rotate coordinates. For example, if you want to rotate a point with coordinates (x, y) by k degrees, you can use the following code:
import cmath
import math
def rotate_point(x, y, k):
z = complex(x, y)
theta = math.radians(k)
rotated_z = z * cmath.exp(complex(0, theta))
return round(rotated_z.real, 10), round(rotated_z.imag, 10)
x, y = 1, 0
k = 45
rotated_x, rotated_y = rotate_point(x, y, k)
print(f"rotated point: ({rotated_x}, {rotated_y})")Rotating the point (1, 0) by 45 degrees gives an approximate result of (0.707, 0.707).
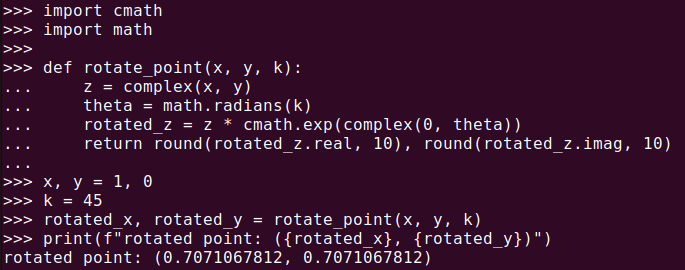
complex() function for coordinate rotationIn addition to this, complex numbers are extremely useful in fields like electrical engineering and signal processing. They are used to represent voltage, current, impedance, and other electrical characteristics, making calculations easier.
Precautions: Type of Real and Imaginary Parts
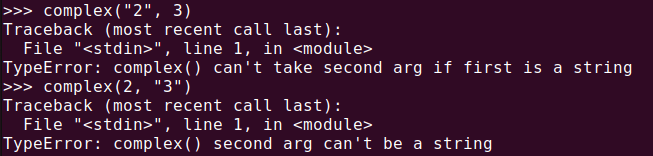
The real and imaginary parts provided to the complex() function must be integers or floats. If other data types are input, an error will occur.
complex("2", 3)
complex(2, "3")For the first line, Python will raise a “TypeError: complex() can’t take second arg if first is a string”, indicating that the first argument cannot be a string. Similarly, the second line will result in “TypeError: complex() second arg can’t be a string”, stating that the second argument cannot be a string.
complex() functionSummary
Python complex() function is a powerful tool for easily creating and handling complex numbers. You can separately manage the real and imaginary parts and perform arithmetic operations between complex numbers. Additionally, complex numbers are essential in fields like electrical engineering, where they simplify the solving of complex problems.
When working with complex numbers, be sure to follow the input format of the complex() function and be cautious about using strings as inputs. Now, you should be able to freely use complex numbers in Python and tackle a wider range of problems.
