Python complex() 組み込み関数を使用すると、複素数を簡単に扱うことができます。Pythonで数学的な演算を行う際に、複素数を使用しなければならない場合があります。複素数は実数(real number)と虚数(imaginary number)で構成されており、これを使うことで様々な数学的な問題を解決することができます。本記事では、complex() 関数の基本的な使い方から、様々な応用方法を説明します。
目次
Python complex() 関数とは?
complex() 関数は、Pythonで複素数を生成するために使用されます。複素数は実数部(real part)と虚数部(imaginary part)で構成されており、虚数は通常「i」で表されますが、Pythonでは「j」または「J」を使用します。複素数は次の形式で表すことができます。
a + bjここで、aは実数部、bは虚数部を表します。
基本的な使い方
complex() 関数は2つのパラメータを取ることができます。1つ目のパラメータは実数部、2つ目は虚数部です。例えば、実数2と虚数3を持つ複素数を生成するには、次のように書きます。
z = complex(2, 3)
print(z)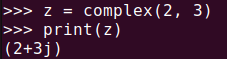
もしパラメータを1つだけ渡した場合、それは実数部と見なされ、虚数部は自動的に0に設定されます。
z = complex(4)
print(z)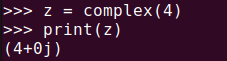
また、文字列を使って複素数を生成することもできます。
z = complex("2+3j")
print(z) # output: (2+3j)実数部と虚数部の分離
複素数から実数部と虚数部をそれぞれ分離する方法は非常に簡単です。複素数オブジェクトは real と imag という属性を持っており、それらを使って実数部と虚数部にアクセスできます。
z = complex(5, 8)
print("実数部:", z.real) # 出力: 実数部: 5.0
print("虚数部:", z.imag) # 出力: 虚数部: 8.0このように、実数部と虚数部を個別に確認できるため、複素数をより効率的に扱うことができます。
Pythonでの複素数の活用法
複素数の演算
複素数は、一般的な数学演算のすべてをサポートしています。例えば、加算、減算、乗算、除算などの演算を複素数同士で行うことができます。
z1 = complex(5, 8)
z2 = complex(3, 2)
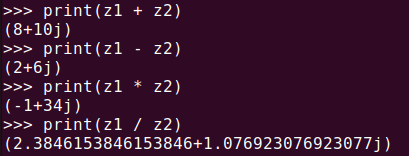
print(z1 + z2)
print(z1 - z2)
print(z1 * z2)
print(z1 / z2)このように、複素数同士の基本的な数学演算はPythonで非常に簡単に処理できます。
複素数の絶対値を求める
複素数の絶対値は abs() 関数で求めることができます。複素数の絶対値は、原点からその複素数までの距離を意味し、その計算式は次の通りです。
|z| = sqrt(a^2 + b^2)ここで、aは実数部、bは虚数部です。Pythonで abs() 組み込み関数を使用して複素数の絶対値を求める方法は以下の通りです。
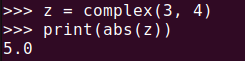
z = complex(3, 4)
print(abs(z))これはピタゴラスの定理を使って計算された結果と同じです。
より複雑な応用例: 座標の回転
次に、座標の回転にも使用することができます。(x, y) の座標を k度だけ回転させたい場合、次のようなコードを使用できます。
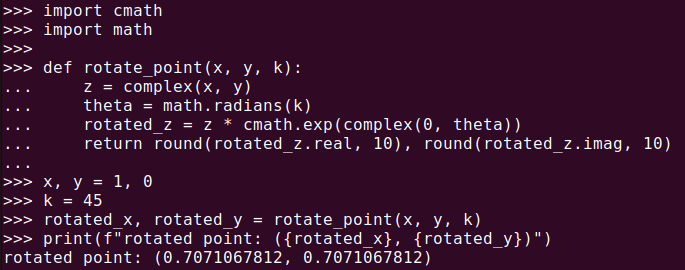
import cmath
import math
def rotate_point(x, y, k):
z = complex(x, y)
theta = math.radians(k)
rotated_z = z * cmath.exp(complex(0, theta))
return round(rotated_z.real, 10), round(rotated_z.imag, 10)
x, y = 1, 0
k = 45
rotated_x, rotated_y = rotate_point(x, y, k)
print(f"rotated point: ({rotated_x}, {rotated_y})")(1, 0) の座標を45度回転させた結果は、約 (0.707, 0.707) であることが確認できます。
また、複素数は電気工学や信号処理の分野でも非常に有用です。電圧、電流、インピーダンスなどの電気的特性を複素数で表現することで、簡単に計算が可能になります。
注意事項: 実数と虚数のタイプ
complex() 関数に渡される実数部と虚数部は、整数型または浮動小数点型でなければなりません。もし他のデータ型を渡すと、エラーが発生する可能性があります。
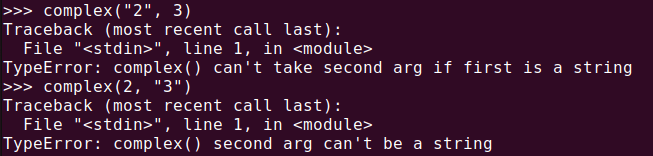
complex("2", 3)
complex(2, "3")1行目の場合、”TypeError: complex() can’t take second arg if first is a string” というエラーが発生し、最初の引数に文字列を使用できないことが示されます。2行目では、”TypeError: complex() second arg can’t be a string” というエラーが発生し、2番目の引数にも文字列を使用できないことが示されます。
まとめ
Pythonのcomplex() 関数は、複素数を簡単に生成し、扱うための強力なツールです。実数部と虚数部をそれぞれ分離して使用でき、複素数同士の数学的な演算も可能です。また、電気工学などの特定分野では、複素数が重要な概念であり、これを活用することで、複雑な問題を簡単に解決することができます。
複素数を扱う際は、complex() 関数の入力形式と、文字列入力時の注意点を忘れないようにしましょう。これで、皆さんもPythonで複素数を自由に使用し、さらに多くの問題を解決できるようになるでしょう。
